Observable
Using the observer pattern for event-driven applications
The EVL core provides a simple yet flexible support for implementing the observer design pattern in your application, based on the Observable element. The Observable receives a stream of so-called notices, which may be events, state changes or any data which fits within a 64bit word, delivering them as notifications (with additional meta-data) to subscribed threads called observers, when they ask for it. Subscribers do not have to be attached to the EVL core, any thread can observe an Observable element. Whether the threads which produce the events, the Observable and the observers live in the same or different processes is transparent.
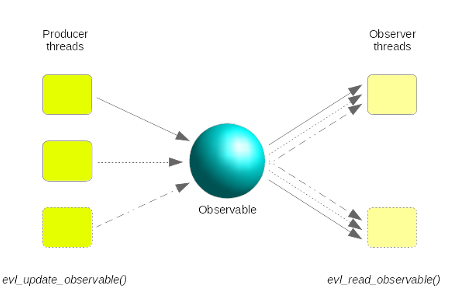
Broadcast mode
By default, an Observable broadcasts a copy of every event it receives to every subscribed observer:
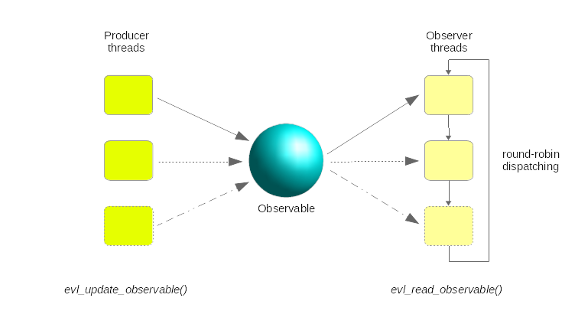
Unicast mode
In some cases, you may want to use an Observable to dispatch work submitted as events to the set of observers which forms a pool of worker threads. Each message would be sent to a single worker, each worker would be picked on a round-robin basis so as to implement a naive load-balancing strategy. Setting the Observable in unicast mode (see EVL_CLONE_UNICAST) at creation time enables this behavior:
Creating an Observable
This call creates an Observable element, returning a file descriptor representing the new object upon success. This is the generic call form; for creating an Observable with common pre-defined settings, see evl_new_observable().
An Observable can operate either in broadcast or unicast mode:
-
in broadcast mode, a copy of every event received by the Observable is sent to every observer.
-
in unicast mode, each message received by the Observable is sent to a single observer. The subscriber to send a message to is picked according to a simple round-robin strategy among all observers.
A set of creation flags for the new element, defining its visibility and operation mode:
-
EVL_CLONE_PUBLICdenotes a public element which is represented by a device file in the /dev/evl file hierarchy, which makes it visible to other processes for sharing. -
EVL_CLONE_PRIVATEdenotes an element which is private to the calling process. No device file appears for it in the /dev/evl file hierarchy. -
EVL_CLONE_UNICASTenables the unicast mode for the Observable. -
EVL_CLONE_NONBLOCKsets the file descriptor of the new Observable in non-blocking I/O mode (O_NONBLOCK). By default,O_NONBLOCKis cleared for the file descriptor.
A printf-like format string to generate the Observable name. See this description of the naming convention.
The optional variable argument list completing the format.
evl_create_observable() returns the file descriptor of the newly created Observable on success. Otherwise, a negated error code is returned:
-
-EEXIST The generated name is conflicting with an existing Observable name.
-
-EINVAL Either flags is wrong, or the generated name is badly formed.
-
-ENAMETOOLONG The overall length of the device element’s file path including the generated name exceeds PATH_MAX.
-
-EMFILE The per-process limit on the number of open file descriptors has been reached.
-
-ENFILE The system-wide limit on the total number of open files has been reached.
-
-ENOMEM No memory available.
-
-ENXIO The EVL library is not initialized for the current process. Such initialization happens implicitly when evl_attach_self() is called by any thread of your process, or by explicitly calling evl_init(). You have to bootstrap the library services in a way or another before creating an EVL Observable.
#include <evl/observable.h>
int create_new_observable(void)
{
int efd;
efd = evl_create_observable(EVL_CLONE_PUBLIC|EVL_CLONE_UNICAST, "name_of_observable");
/* skipping checks */
return efd;
}
This call is a shorthand for creating a private observable operating in broadcast mode. It is identical to calling:
evl_create_observable(EVL_CLONE_PRIVATE, fmt, ...);
Note that if the generated name starts with a
slash (’/’) character, EVL_CLONE_PRIVATE would be automatically turned
into EVL_CLONE_PUBLIC internally.
Working with an Observable
Once an Observable is created, using it entails the following steps, performed by either the thread(s) issuing the stream of events to the Observable, or those observing these events:
Observers need to subscribe to the Observable. Observers can subscribe and unsubscribe at will, come and go freely during the Observable’s lifetime. Depending on its subscription flags, the observer may ask for merging consecutive identical notices or receiving all of them unfiltered (See EVL_NOTIFY_ONCHANGE).
Event streamers can send notices to the Observable by calling evl_update_observable().
Observers can read notifications from the Observable by calling evl_read_observable().
Once an Observable has become useless, you only need to close all the file descriptors referring to it in order to release it, like for any ordinary file.
This call sends up to nr notices starting at address ntc in memory to the Observable referred to by efd. This call never blocks the caller. It may be used by any thread, including non-EVL ones.
A notice contains a tag, and an opaque event value. It is defined by the following C types:
union evl_value {
int32_t val;
int64_t lval;
void *ptr;
};
struct evl_notice {
uint32_t tag;
union evl_value event;
};
All notices sent to the Observable should carry a valid issuer tag in
the evl_notice.tag field. For applications, a valid tag is an
arbitrary value greater or equal to EVL_NOTICE_USER (lower tag
values are reserved to the core for HM diag codes).
evl_update_observable() returns the number of notices which have been successfully queued. Each notice which have been successfully queued for consumption by at least one observer counts for one in the return value. Zero is returned whenever no observer was subscribed to the Observable at the time of the call, or no buffer space was available for queuing any notification for any observer. Otherwise, a negated error code is returned on error:
-
-EBADF efd is not a valid file descriptor.
-
-EPERM efd does not refer to an Observable element. This may happen if efd refers to a valid EVL thread which was not created with the
EVL_CLONE_OBSERVABLEflag. -
-EINVAL Some notice has an invalid tag.
-
-EFAULT if ntc points to invalid memory.
Sending a notice to an observable
void send_notice(int ofd)
{
struct evl_notice notice;
int ret;
notice.tag = EVL_NOTICE_USER;
notice.event.val = 42;
ret = evl_update_observable(ofd, ¬ice, 1);
/* ret should be 1 on success. */
}
This call receives up to nr notifications starting at address nf
in memory from the Observable referred to by efd. It may only be
used by observers subscribed to this particular
Observable. If O_NONBLOCK is clear for efd, the caller might block
until at least one notification arrives.
A notification contains the tag and the event value sent by the issuer of the corresponding notice, plus some meta-data. A notification is defined by the following C type:
union evl_value {
int32_t val;
int64_t lval;
void *ptr;
};
struct evl_notification {
uint32_t tag;
uint32_t serial;
int32_t issuer;
union evl_value event;
struct timespec date;
};
The meta-data is defined as follows:
-
serial is a monotonically increasing counter of notices sent by the Observable referred to by efd. In broadcast mode, this serial number is identical in every copy of a given original notice forwarded to the observers present.
-
issuer is the pid of the thread which issued the notice, zero if it was sent by the EVL core, such as with HM diagnostics.
-
date is a timestamp at receipt of the original notice, based on the built-in EVL_CLOCK_MONOTONIC clock.
evl_read_observable() returns the number of notifications which have been successfully copied to nf. This count may be lower than nr. Otherwise, a negated error code is returned on error:
-
-EAGAIN
O_NONBLOCKis set for efd and no notification is pending at the time of the call. -
-EBADF efd is not a valid file descriptor.
-
-EPERM efd does not refer to an Observable element. This may happen if efd refers to a valid EVL thread which was not created with the
EVL_CLONE_OBSERVABLEflag. -
-ENXIO the calling thread is not subscribed to the Observable referred to by efd.
-
-EFAULT if nf points to invalid memory.
Receiving a notification from an observable
void receive_notification(int ofd)
{
struct evl_notification notification;
int ret;
ret = evl_read_observable(ofd, ¬ification, 1);
/* ret should be 1 on success. */
}
Events pollable from an Observable
The evl_poll() and poll(2) interfaces can monitor the following events occurring on an Observable:
-
POLLINandPOLLRDNORMare set whenever at least one notification is pending for the calling observer thread. This means that a subsequent call to evl_read_observable() by the same thread would return at least one valid notification immediately. -
POLLOUTandPOLLWRNORMare set whenever at least one observer subscribed to the Observable has enough room in its backlog to receive at least one notice. This means that a subsequent call to evl_update_observable() would succeed in queuing at least one notice to one observer. In case multiple threads may update the Observable concurrently, which thread might succeed in doing so cannot be determined (typically, there would be no such guarantee for the caller of evl_poll() and poll(2)).
In addition to these flags, POLLERR might be returned in case the
caller did not subscribe to the Observable,
or some file descriptor from the polled set refer to an EVL thread
which was not created with the
EVL_CLONE_OBSERVABLE flag.
Observing EVL threads
An EVL thread is in and of itself an Observable element. Observability
of a thread can be enabled by passing the EVL_CLONE_OBSERVABLE flag
when attaching a thread to the EVL core. In this case, the file
descriptor obtained from evl_attach_thread() may be
subsequently used in Observable-related operations. If the thread was
also made public (EVL_CLONE_PUBLIC), then there
is a way for remote processes to monitor it via an access to its
device.
Threads can monitor events sent to an observable thread element by subscribing to it. An observable thread typically relays health monitoring information to subscribers. An observable thread can also do introspection, by subscribing to itself then reading the HM diagnostics it has received.
